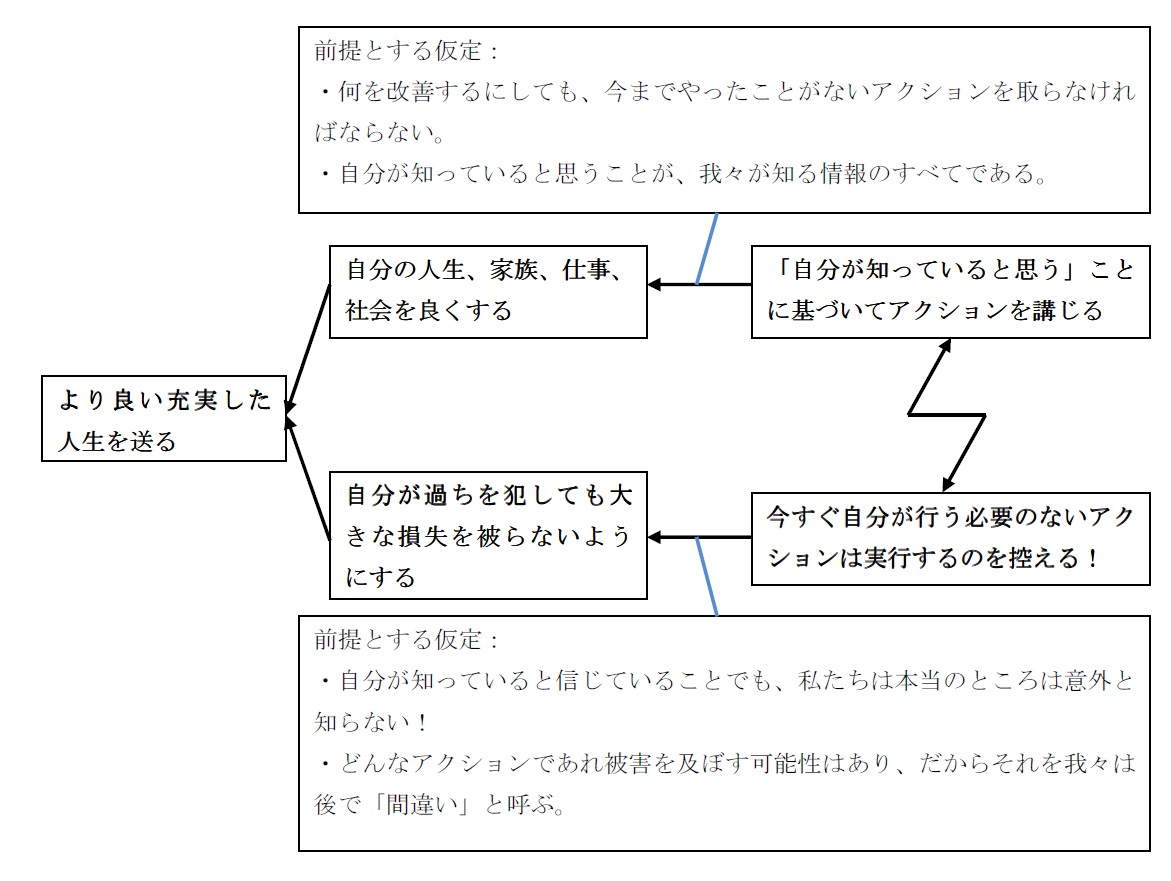
この「クラウド(対立解消図)」は、知識が限られた現実に生きる我々の一般的な対立(またはジレンマ)を表現したものです。ゴールドラット博士は「決して知っているとは言わない」という警句を作って、今現在の我々の理解に疑問を投げる兆候を常に探して、新たなパフォーマンスの飛躍の準備をしておけと教えました。しかし問題は、知識の限界を認めることは、しなくてよいことは何もせず済ますために、自分の「居心地の良いゾーン」の外の意思決定は一切しないという、麻痺症状を引き起こすかもしれないことです。自分の快適ゾーンでしか策を講じないのは、対立に対する妥協の蔓延に繋がります。
気持ちよくないこともあったが、幸運にもゴールドラット博士と親しく仕事をする中で、彼の突っ込んだ質問に「私は知らない」と答えるのは、非常に感動的な体験でした。そう言うと彼はいつも怒って、不完全でも自分が何を知っているか、そしてそれが我々の最善の答えを得るのにどう役立つのか、言葉にしろと迫ったのでした。ゴールドラット博士に言わせれば、何も知らない唯一の理由は無関心だという。少しでも気に留めようと思えば、たとえ相当不確かでも、論理的にある一定の結論を導き出せるような、ある特定の結果に気づくはずだと言うのです。この経験から私は次の警句に辿り着きました:
決して何も知らないとは言わない
この理解は先に述べた対立よりさらに鋭いパラドックスです。知っていると同時に知らないって?
このパラドックスに対する私の解は、意思決定に関する限り、不確実性の大きさの幅を認めて、我々の知識には「まあ十分知っている」と信じる部分と知らないと分かっている部分の2つがあると認めることです。そういうわけで、ここで述べた2つの対立に付け加えないといけない要素は、ある程度の確かさで知っていると思うことを表現した「完全ではないがまあ十分」という言葉であり、稀に間違っていることもある事実を受け入れることです。
しかし、ほぼ真実でないことを予測するとなれば、まあ十分確かな知識での判断は、もっとずっと具体的なはずです。その例をいくつか見てみましょう。
- スポーツチームが2チームある。今のところ、Aチームは10勝0敗、Bチームは0勝10敗。 どっちが勝つか?
- Bが勝つということはまず無いだろうと思ってよい。
- (サッカーのように)ドローもありなら、ドローはまあ考えてもいいかもしれない。
- また、どういう結果はまずないという判断も可能。たとえば、バスケットボールで100対0はまあない。勘のいい人なら60点差以上で勝つことはまず無いとさえ言うかもしれない。どういう結果がまずないというこの判断は、何が十分ありそうかには大きな自由度を残しており、我々が知らないことの妥当な境界の線引きは我々に委ねている!
- 経済成長率の予測。
- 過去と市場の理解に基づいた現在の知識全体の帰結として、どれくらいの成長率はまあ高すぎで、逆にどれくらいの成長率はまあ低すぎかという概算が出る。それは、実際どの結果になるかは分からなが起き得る結果の十分確かな範囲を示す。
- 新しいC級の役員の任命。
- 我々は失敗しない者を選びたい! つまり、候補者が失敗することはまずないことが選考条件だ。ということは、他の者より高い目標を達成するのはまず確かだが、失敗して深刻な損失を出すかもしれないと思う候補者は、選考から外れる可能性がある。
ということで、何はまず真実ではないという認識があっても、我々がまず確かだと信じる知識が間違っていることも、比較的稀だが時々ある事実を我々は認めます。
因みに、知っていると知らないの境界は、ほぼそうなるのは確かだと思うが、実際どれになるかまでは分からないケースをすべて含みます。それは自分の視点でみた不確実性の境界でもあります。私は、不確実性とは私が知らないすべてだと思っています。意思決定のプロセスでは、我々が知らない境界線の内にある潜在的な結果すべての起き得る可能性を真剣に検討して、それらすべての結果の潜在的な利益と損失の範囲を想定しないといけません。
ところで、TOCは販売予測には反対であり販売予測を必要としないと思われています。私はその認識には異論があります。
予測の本当の問題は、予測からどんな情報が得られるかに対する根本的な誤解です。どれくらいの売上(以上、以下)はまずあり得ないか伝えるには販売予測が絶対に必要で、そのお陰で私たちは、ほぼ確かな需要の範囲に事前に備えておけるのです。
TOCの在庫補充ソリューション(Replenishment solution)に従って、製品Aの目標在庫を100個だと仮定しましょう。現在の手持ち在庫は30個、手配中の補充指示は2件でそれぞれ40個と30個だとします。(訳注:手持ちと手配中の在庫の合計は目標在庫と同じ100個になっている)
バッファ管理は、今現在の手持ち在庫がレッドゾーンであることを教えてくれます。それは、翌日か翌々日の内に需要が30個を超える可能性が高いという予測がまあ妥当だろうということです。ですので、次届く予定の補充を督促しないといけません。とは言っても、明日急に需要が140個を超えることはまずないだろうと考えられます! つまり、通常の供給リードタイム内に需要が目標在庫を超えることはまずないだろうという予測、それがTOCで用いる予測なのです!
最大の競合が3、4日の内に廃業しそうだという噂を聞いたとしましょう。それは「噂」であって厳然たる事実ではないのですが、大きな影響を及ぼす可能性が高い事態が本当に起きて、重大な意思決定をせざるを得なくなった状況に直面したことは、これまで何度ありますか? あなたは、その噂は「本当でもおかしくない」と感じて、それが現実になれば自社の製品の需要が伸びると予測したとしましょう。
あなたは噂に基づく予測を根拠にして行動を起こしますか?
噂はニセ情報である可能性もあるので、私ならおそらく、まったく需要が伸びなくても、過剰産生であまり大きな損失を被らないよう、非常に慎重にやるだろうと思います。
これは、一部知っていると同時に一部知らない不確実な現実を生きる本質です。ですから、私たちは、失敗してもあまり深刻すぎる打撃を受けず、ほとんどの場合は大きな利益が得られるような意思決定をすべきなのです。
著者:エリ・シュラーゲンハイム
飽くなき挑戦心こそが私の人生をより興味深いものにしてくれます。私は組織が不確実性を無視しているのを見ると心配でたまりませんし、またそのようなリーダーに盲目的に従っている人々を理解することができません。
この記事の原文: “Never Say I Know” and the Limitations of our (Reasonable) Knowledge